Mathematical and Physics Concepts in Computer Games
| ✅ Paper Type: Free Essay | ✅ Subject: Computer Science |
| ✅ Wordcount: 2570 words | ✅ Published: 29 Aug 2017 |
- Introduction
A two part assignment was distributed and part one was run a simulation of a given differential equation using numerical integration techniques i.e. Euler and 4th order Runge-Kutta methods. Also continued as part one a table showing the results of the simulation was to be produced and each value was to be to 3 decimal places. Two graphs where to be produced a) a plot of each simulation result and the exact solution b) a plot of error values in each simulation and a short analysis of the results was to be produced. Part two a little more complicated than part one was to implement realistic physics of a rocket movement in earth atmosphere.
- Part 1
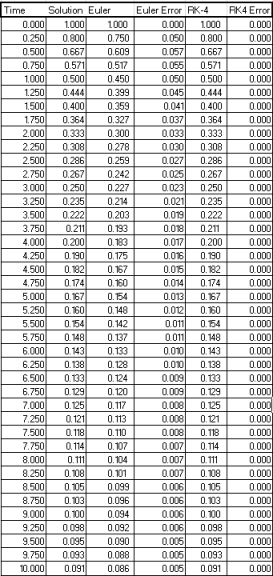
To calculate the exact solution was the simplest of equations mostly because it was provided it was a matter of processing the data. In simple terms to calculate the exact equation was displayed such as 1/(1+t), whereas t is time and increments by 0.25 each solution, therefore the equation would look like 1/(1+0.25) = 0.8 and the next step is 1/(1+0.50) = 0.667, furthermore is quite easy to calculate this equation.
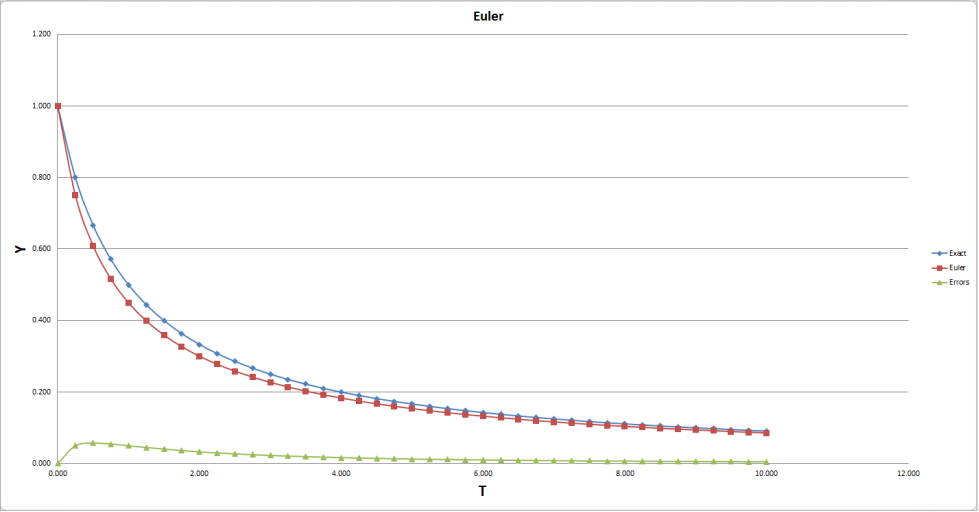
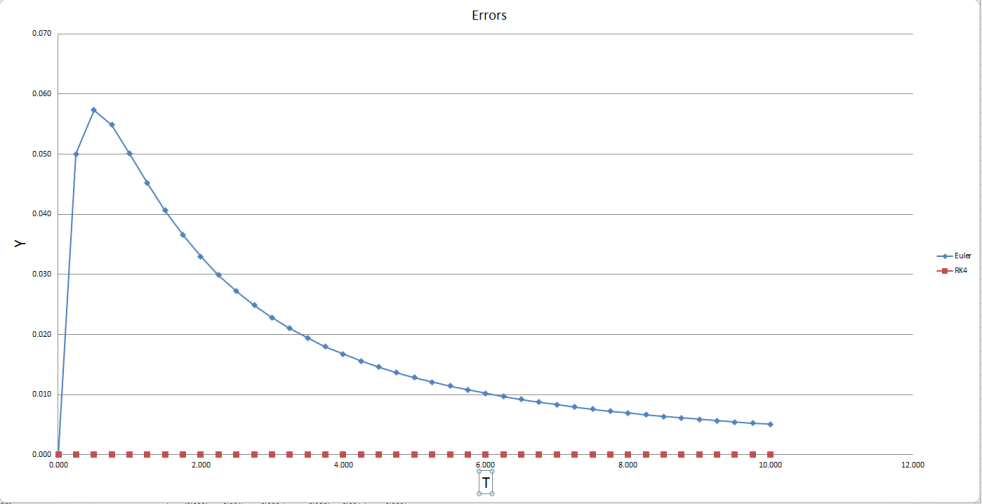
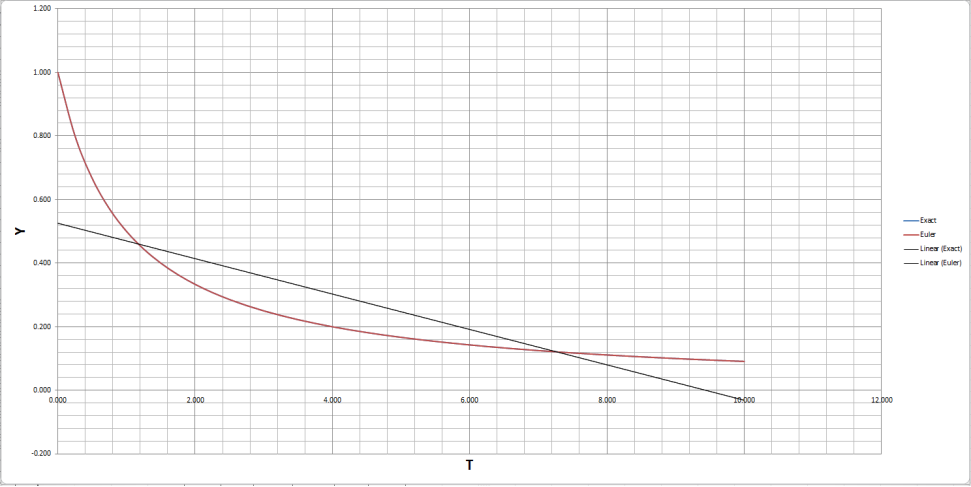
From the results appendix [a1] there are noticeable differences between Euler and the exact solution, first of all for Euler’s method I used y-1+-(y-1^2)*(h), loosely translated into simpler terms y-1 is the previous y coordinate + -previous y coordinate to the power of 2 multiplied by h which in this case h was equal to 0.25. After having solved the equation for each t i.e. the x coordinate a significant difference was noticeable. After calculating Euler’s results next was to calculate Euler’s errors including the first y coordinate which was equal to 1 therefore the exact solution for the first y coordinate was also equal to 1 so there would be an error equal to 0 as the result. However the rest of the results varied but still remained below their equal t (x) coordinate for example t 0.250 was equal to y 0.800 in the exact solution and 0.750 in Euler’s, after analysing the rest of the results prior to the calculation it was clear each Euler y result was lower than the exact solution y coordinate and was fairly easy to come to the error by simply exact solution y – Euler solution y. Upon summing up all of Euler’s results it gives a solution of 0.761 and dividing that by 41 gives a solution of 0.019. The reason it was divided by 41 is because there are 41 y coordinates including the first y coordinate which is equal to 1, therefore revealing the average number Euler error, suggesting Euler’s method missed out on the exact solution at an estimate of 0.019, this does not seem a big difference but when trying to implement real physics in a game it makes all the difference. The graphs in appendix [a3] shows the simulation for Euler’s method and the exact solution where it is easy to see each y coordinate and each error coordinate whereas [a4] shows the closer Euler’s line and the exact line get to each other as t (time), (x coordinate) ascends, this suggests that Euler’s method becomes more accurate over time and after using Euler’s method for a long period of time eventually Euler’s would’ve matched the exact solution at some point. Having viewed [a3] and [a4], [a8] shows the linear line for the exact solution and the linear line for Euler’s method.
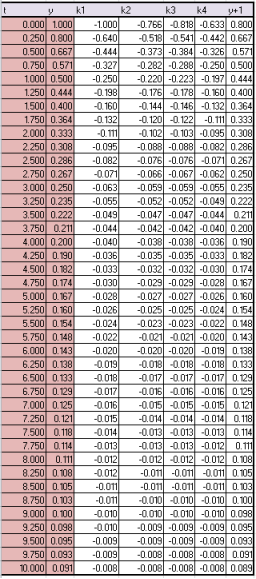
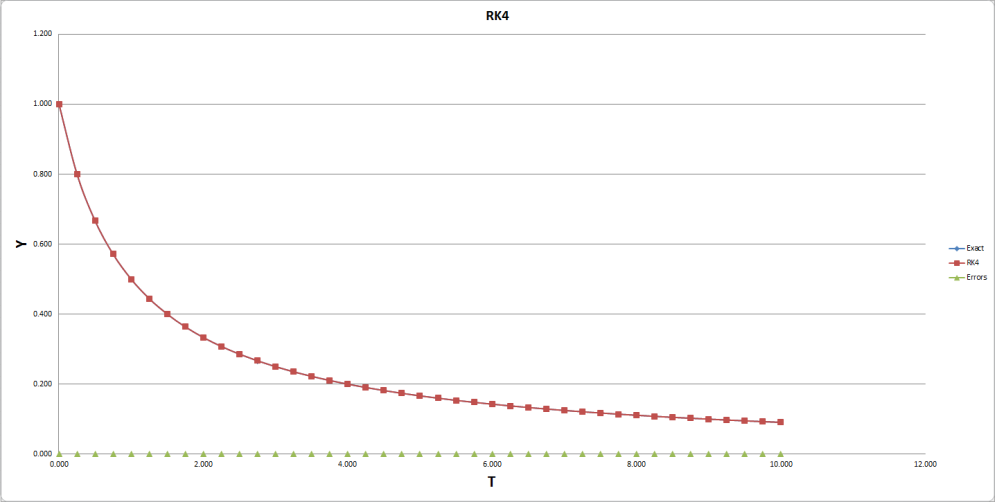
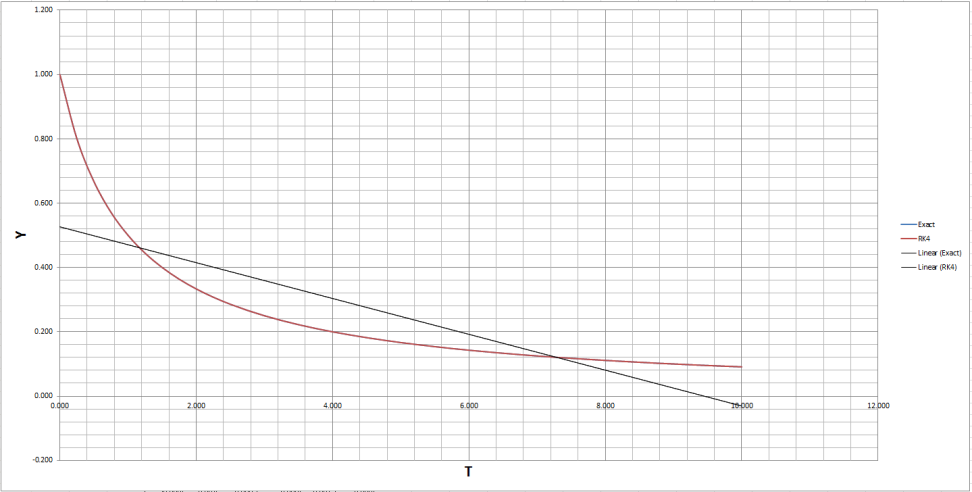
4th Order Runge-Kutta method was more complicated than Euler’s mostly because as shown in [a1] the solution is more accurate because of the slopes that must be calculated in order to solve each y coordinate see [a2] for each slope solution. First and foremost we start by solving the first slope as k1 which was calculated as -(y-1^2) and like Euler’s method translate to minus (the previous y coordinate to the power of 2) that’s how k1 was solved. K2 has bit more calculation to process which looks like -(y-1+(0.5*k1-1*h))^2) translated to simpler terms is minus(previous y plus (0.5 multiplied by previous k1 multiplied by 0.25)) to the power of 2) this is how the second slope is discovered, solving k3 is much simpler because k1-1 is replaced with k2-1 the previous k1 solution that was just solved and k4’s calculation becomes smaller -(y-1+(k3-1*h)) to the power of 2) just like k2 and k3, k4 using k3’s previous solution that was solved. The fun part is finding y+1 which is the next y coordinate per t coordinate the calculation used is (y-1+((1/6)*(k1-1+2*(k2-1)+2*(k3-1)+k4-1)*h)) a significantly long calculation but reliable as it will get close to the exact solution result, translated it is (previous y coordinate plus(1 divided by 6) multiplied by (previous k1 solution plus 2 multiplied by (previous k2 solution) plus 2 multiplied by (previous k3 solution) plus (previous k4 solution) multiplied by 0.25). The sum of RK4 errors are 0 and the average was equally 0 that is an incredibly accurate method but more complicated to solve as Euler’s method is the simplest RK method (first order) which is why RK4 is more accurate as it is a multi-stage method. See appendix [a5] for each y coordinate because RK4 method was incredibly accurate the exact solution coordinates cannot be seen but the data types are there to see and the legend is also there to show the different styles between each coordinate, appendix [a6] show the curve without any coordinate markers on them, again the curves cannot be distinguished from each other because of RK4’s incredible accuracy. See appendix [a7] to see the error coordinates for each integration technique on the same graph; it is quite easy to see which method is much more accurate but again this is because Euler’s method is a first order method whereas Runge-Kutta is a fourth order method, Runge-Kutta’s method has more steps in solving the equations therefore providing for a more accurate solution and producing less error values, whereas Euler’s method only has one step and will always provide an error value each time. See [a9] for the linear line of the exact solution and RK4 estimation, it is extremely difficult to see because RK4 method is so accurate.
Part 2
After using RK4 in part 1 an understanding it had taken some time to put it into physics, however the following scenario seems to be correct.
The equation for acceleration is a = (Force Rocket + Force Drag) – mass.
The equation for Force drag is force drag = -0.5 * (0.2^3) * (0.2) * (20^2) * (2^2) ^2
The time step that is used is 1 i.e. 1kg m^2 because that is how much it can increment or decrement by with the user input. Time will go up to 60, the max the rocket’s force can go up to is 20kg m^2 and because acceleration is a derivative of velocity k1 = (time + velocity) i.e. the x and y positions. To find k2 the equation was k2 = (time + 0.5 * h, velocity + k1 * h), to find k3 is the same as k2 except the k1 in the equation is replaced with k2. K4 the last slope is calculated as k4 = (time + h, velocity + k3 * h). Lastly acceleration is calculated as a1 (next acceleration value) = (a-1 (previous value) + 1/6(k1 + 2 * k2 + 2 * k3 + k4) * h). The hard part is getting the equations correct after that it is a matter of using a loop in game to calculate the player’s position; the player’s position is equal to 5 metres.
Pseudo Code for in game:
Declare Static Class 4th Order Runge-Kutta
{
Do
Declare Delegate double RK (x, y) variables declared as doubles (timer and velocity)
Declare a static variable to calculate 1/6 as fS (fraction sixth)
Declare rocket position as 5
Declare timer
Declare a static double rk4(double x, y, h, RK f) x, y and h are doubles, r is called from delegate variable)
{
Declare half of h as halfh
Declare Double k1, k2, k3, k4
Declare acceleration equals 0
y = acceleration
K1 = (x plus y)
K2 = (x plus halfh multiplied by h) plus (y plus k1 multiplied by h)
K3 = (x plus halfh multiplied by h) plus (y plus k1 multiplied by h)
K4 = (x plus h) plus (y plus k3 multiplied by h)
Return (y plus fS multiplied by (k1 plus 2 multiplied by k2 plus 2 multiplied by k3 + k3))
RK acceleration equals y^2
^^^ Returns acceleration
}
Declare Force drag kg to the power of 2 = -0.5 multiplied by (1.2 to the power of 3) multiplied by (0.2) multiplied by (20 to the power of 2) multiplied by (y to the power of 2 per second) because y is velocity
Acceleration = (timer + force drag) / mass (decrement mass by 1 every second))
Player position plus acceleration every second
If key pressed equals up
Increment acceleration by 1
Else if key press equals down
Decrement acceleration by 1
Print timer, player position, acceleration and y
While timer is less than 60
}
Flowchart























Critical analysis of the use of numerical integration techniques to solve similar situations in game development
In the context of differential equations no numerical integration method is known as the method that is the best method to solve any and all ordinary differential equations. It all depends on the type of equation that is presented. When discussing gaming physics the solution to the differential equations plays a big part in games taking on more realism for example if a player fires an arrow in the air from a crossbow depending on velocity, gravity and wind etc. When and where will the arrows new position be within the game environment? Physics can be found almost anywhere whether it is in Skyrim shooting an arrow that will eventually drop or sniping in Battlefield that also includes bullets descending over time which is incredible and makes the games more realistic and much more difficult. Before using any method some basic equations must be known first for example force = mass multiplied by acceleration and acceleration = force divided by mass, standard equations that can be learned just using a search engine. Next the derivative of velocity is acceleration and the derivative of acceleration is position, a derivative is “something which is based on another source” [1]
There are several methods to choose from when it comes to differential equations:
- First order integration
- Higher order integration
First order integration
Euler’s Method
One of the rather simpler methods that game developer can use although as already seen above it is not the most accurate. [2] Just like the previous ordinary differential equation that was solved in part one a developer takes the initial position and velocity and calculates the next position and velocity over time, a time step is used to calculate the next position and velocity such as the previous one that was used 0.25, once the first value is calculated the method is simply repeated to calculate the next one. An equation could look like this Vn+1 = Vn + (An *dt) whereas V is velocity and A is acceleration then the position could be calculated like Pn+1 = Pn + (Vn *dt) whereas P is position. Although this is a simpler method to use an error value will always be return because it is not the most accurate to produce solutions. Using any method can produce error values which is why the numerical integration methods provide estimations and not exact solutions whereas as the error value calculates how far off the estimation was from the exact solution. According to Bourg [3] instability is eliminated or minimized by smaller step sizes however larger steps size seems to make the problem much more complicated than it needs to be. Stability plays an important part for calculating equations more calculations will be processed if the step size is significantly small however this results in more stability. Bourg [3] mentions an adaptive step size where after a predicted amount of error the step size is changed as calculations are being processed. To use adaptive step size method it has to be based on the errors given from the estimations by doubling the step size, Heidt’s [4] mentions in his abstract the adaptive step size method works considerably well with second-order split-step Fourier integration scheme and can be greatly improved when using it alongside 4th order Runge-Kutta method. Unless the error values provided by Euler’s estimations causes a serious change in a games physics then there should be no problem using Euler’s method for simpler equations [2]. The simplest way to estimate the exact solution is using Euler’s method, when using the method and there is a big difference between y1 and y-1, setting aside the curvature the linear extrapolation will not match up to it.
Higher Order Integration
4th Order Runge-Kutta
Runge-Kutta is more commonly used in physics [2], this integration method is incredibly accurate from what has been displayed already in part one of this report due to the method have many more steps to solving equations. The accuracy is second to none because RK4 calculates equations estimations in four steps thus given the name 4th Order. In order to achieve this accuracy a price must be paid and the price is more calculations need to be processed to calculate the physics; it has many more computations than other integrator techniques [2]. These types of calculations only need to be considered when accuracy is a must in games like bouncing a grenade of a doorframe in call of duty, therefore not all physics in games will require RK4 to calculate physics because physics is different in all games and some will only require Euler’s method. So using the example of the Rocket in earth’s atmosphere a = Fr + Fd / m translates to acceleration = (FORCE rocket + FORCE drag) divided by mass. The rocket force increments by 1kg/m2 every time the user presses the UP key on the keyboard. Fr is calculated as Fd = -0.5.P.Cd.A.v^2 so basically force drag = minus 0.5 multiplied by P (airdensity) multiplied by Cd (Drag coefficient) multiplied by A (frontal area of the rocket) multiplied by v (velocity) squared.
Conclusion
All in all no numerical integration technique is better than the other it all depends what kind of physics in games needs to be produced, if it’s simple physics where the estimation does not make a major impact on the outcome Euler’s method is the way to go for its quick computations it can make having simulations processed rather quickly, as for games where more complicated physics is involved 4th Order Runge-Kutta is the next best thing although it takes many more computations to be calculated the estimates are near perfect, RK4 is second to none when it comes to accuracy because of the extra work that needs to be considered. For example in games like battlefield RK4 is most likely to be used for those physics because the estimations need to be as accurate as can be, this takes into account bullet drop and flying aircrafts.
Appendix
[a1]
[a2]
[a3]
[a4]
[a5]
[a6]
[a7]
[a8]
Euler
[a9]
Rk4
References
[1]https://www.google.co.uk/?gfe_rd=cr&ei=xfluWI62OrLS8AerrruIDA&gws_rd=ssl#q=what+is+a+derivative (Accessed: 18 December 2016).
[2] Dickinson, J. (2015) Numerical integration in games development. Available at: https://jdickinsongames.wordpress.com/2015/01/22/numerical-integration-in-games-development-2/ (Accessed: 20 December 2016).
[3] Bourg, D.M. (2001) Physics for games developers. United States: O’Reilly Media, Inc, USA (Accessed: 25 December 2016)..
[4] Heidt, A.M. (2009) ‘Efficient Adaptive step size method for the simulation of Super continuum generation in optical fibres’, Journal of Light wave Technology, 27(18), p. 1. doi: 10.1109/jlt.2009.2021538 (Accessed: 2 January 2017).
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allDMCA / Removal Request
If you are the original writer of this essay and no longer wish to have your work published on UKEssays.com then please click the following link to email our support team:
Request essay removal



